Productos Notables.
Son polinomios que se obtienen de la multiplicación entre 2 o mas polinomios que poseen características especiales o expresiones particulares, y cumplen ciertas reglas fijas.
Su resultado puede ser escrito por simple inspección sin necesidad de efectuar la multiplicación o no verificar con la multiplicación.
Cada producto notable corresponde a una formula de factorizacion.
Ejemplo:
(a + b)2 =
(a) (a) = a2 <------- El cuadrado del primer termino
(a2) (b) = 2ab <---------- El doble del primero por el segundo termino
(b) (b) = b2 <---------- El cuadrado del segundo
R= a2 + 2ab + b2 <------- Trinomio cuadrado perfecto.
(x + a) (x + b)
(x2)2 = x4 <---------- El cuadrado del primero
(a + b) = ab <----------- Suma de los terminos no comunes
(ab) (x2) = abx2 <---------- Por el termino común
abx2 + ab = 2a + 2b + x2 <----------- Mas el producto de los no comunes
R= 2a + 2b + x2
Su resultado puede ser escrito por simple inspección sin necesidad de efectuar la multiplicación o no verificar con la multiplicación.
Cada producto notable corresponde a una formula de factorizacion.
Términos:
- Monomio: 1 termino Ejemplo: 2x
- Binomio: 2 términos Ejemplo: x + y
- Trinomio: 3 términos Ejemplo: x + y + z
- Polinomio: 4 o mas términos Ejemplo: 3 + z + y + w
Algunas expresiones de productos notables son:

- Binomio al cuadrado:
El cuadrado del primero mas el doble del primero por el
segundo mas el cuadrado del segundo .
R= Trinomio Cuadrado Perfecto
(a + b)2 =
(a) (a) = a2 <------- El cuadrado del primer termino
(a2) (b) = 2ab <---------- El doble del primero por el segundo termino
(b) (b) = b2 <---------- El cuadrado del segundo
R= a2 + 2ab + b2 <------- Trinomio cuadrado perfecto.
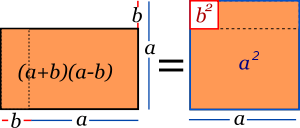
- Binomio conjugado.
El cuadrado del primero menos el cuadrado del segundo.
R= Diferencia de cuadrados
Ejemplo:
(a + b) * (a - b)2 = a2 - b2
(a) (a) = a2 <---------- El cuadrado del primero
(b) (b) = b2 <--------- El cuadrado del segundo
a2 - b2 <--------- El cuadrado del primero menos el cuadrado del segundo termino.
- Binomio con termino común.
El cuadrado del primero mas la suma de los términos no comunes
por el termino común mas el producto de los no comunes
R= Trinimio de la forma x2 + bx + c
Ejemplo:
(x + a) (x + b)- Binomio con termino común.
El cuadrado del primero mas la suma de los términos no comunes
por el termino común mas el producto de los no comunes
R= Trinimio de la forma x2 + bx + c
Ejemplo:
(x2)2 = x4 <---------- El cuadrado del primero
(a + b) = ab <----------- Suma de los terminos no comunes
(ab) (x2) = abx2 <---------- Por el termino común
abx2 + ab = 2a + 2b + x2 <----------- Mas el producto de los no comunes
R= 2a + 2b + x2

No hay comentarios.:
Publicar un comentario