Aprendizajes Esperados:
- Analizar los diversos procesos técnicos para la elección del mas eficiente
- Que los alumnos obtengan modelos geométricos a partir de expresiones algebraicas
Fundamentos
En este tema hablaremos de los tipos de formas en el que se puede utilizar los procesos técnicos que se ven implicados en la vida diaria usando como base las matemáticas, a reconocer términos semejantes y a realizar operaciones básicas con expresiones algebraicas.
Tema: "Expresiones Algebraicas Y Sus Operaciones: suma, resta y multiplicación"
Intención Didáctica:
- Que los alumnos reconozcan y obtengan expresiones algebraicas equivalentes a partir de modelos geométricos.
Contenido:
- Leyes a utilizar
- Suma de expresiones algebraicas
- Ejemplos de suma
- Resta de expresiones algebraicas
- Ejemplos de resta
- Multiplicación de expresiones algebraicas
- Ejemplos de multiplicación
LEYES A UTILIZAR
Ley de signos: El resultado es negativo si la cantidad de factores es impar, de lo contrario es positivo.
(+) (+)= +
(-) (-) = +
(+) (-) = -
(-) (+) = -
Ley de exponentes: El producto de dos o mas potencias de la misma base es igual a la base elevada a la suma de las potencias
(xm) (xn) = xm + n
Ley conmutativa: El orden de los factores no altera el producto
(x) (z) (y) = (y) (z) (x) = (z) (x) (y) = xyz
Ley de los coeficientes: El coeficiente del producto de dos o mas expresiones algebraicas es igual al producto de los coeficientes de los factores.
(4x) (5y) = 4 * 5 * x * y = 20xy
SUMA DE EXPRESIONES ALGEBRAICAS
(MONOMIOS Y POLINOMIOS)
Monomios:
Un Monomio es una expresión algebraica en la que las únicas operaciones que aparecen entre las variables son el producto y la potencia del exponente natural
Para realizar la suma de monomios lo primero en lo que nos debemos de fijar es en los coeficientes y la variables (literales).
Cuando los monomios tiene las variables iguales y su exponente igual solo se agrupan y se suma normalmente el coeficiente.
POLINOMIOS:
Un polinomio es una expresión que contiene muchos términos. Para realizar una suma de polinomios es necesario identificar los Términos Semejantes.
Un termino semejante es aquel en el que sus variables
(y sus exponentes como el 2 en x2) son iguales.
7x x -2x porque las variables son todas x
Para sumar polinomios se realizan dos pasos:
-
Junta todos los términos semejantes
-
Suma los términos semejantes.
Junta todos los términos semejantes
Suma los términos semejantes.
Ejemplos:
MONOMIOS
POLINOMIOS
RESTA DE EXPRESIONES ALGEBRAICAS
MONOMIOS:
Para restar monomios se restan los coeficientes y se deja la misma
parte literal. Hay que tener en cuenta que solamente se pueden restar los
monomios que son semejantes.
axn - bxn = (a - b)xn
POLINOMIOS:
Para restar polinomios se suelen cambiar los signos de todos los términos del polinomio que se restara (+ por -, y - por +) y transformar la resta en suma, ya que restar es lo mismo que sumar el opuesto. Pero también se puede hacer restando los coeficientes del mismo grado.
Ejemplos:
P(x)= 3x5 + 2x3 - 5x2 + 6 y Q(x) =
8x3 + 3x2 - x - 4
P(x) - Q(x)= 3x5 - 6 x3 - 8x2 + x +
10
MULTIPLICACIÓN DE EXPRESIONES ALGEBRAICAS
MONOMIOS:
Se le llama multiplicación de monomios a la multiplicación de un solo termino por otro. Para realizar esta operacion se deben de seguir una serie de reglas:
Reglas:
- Se multiplica el termino del multiplicado por el termino del multiplicado
- Se suman los exponentes de las literales iguales
- Se coloca las literales diferentes en un solo resultado
Para multiplicar dos polinomios lo primero que se debe hacer es: multiplicar cada termino del otro polinomio .Y por ultimo suma los resultados y simplifica si es que se requiere
1 termino por 1 termino (monomio por monomio)
Para multiplicar un termino por otro termino, primero multiplica las constantes, después multiplica cada variable y por ultimo combina el resultado.
1 termino por 2 términos (monomio por binomio)
Multiplica el termino que esta solo por los otros dos términos.
2 términos por 1 termino (binomio por monomio)
Multiplica cada uno de los términos por el que esta solo
2 términos por 2 términos (binomio por binomio)
Cada uno de los términos del primer binomio se multiplica por cada uno de los términos del segundo binomio.
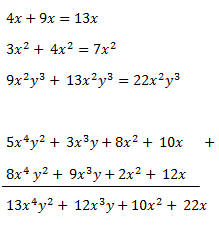
.jpg)
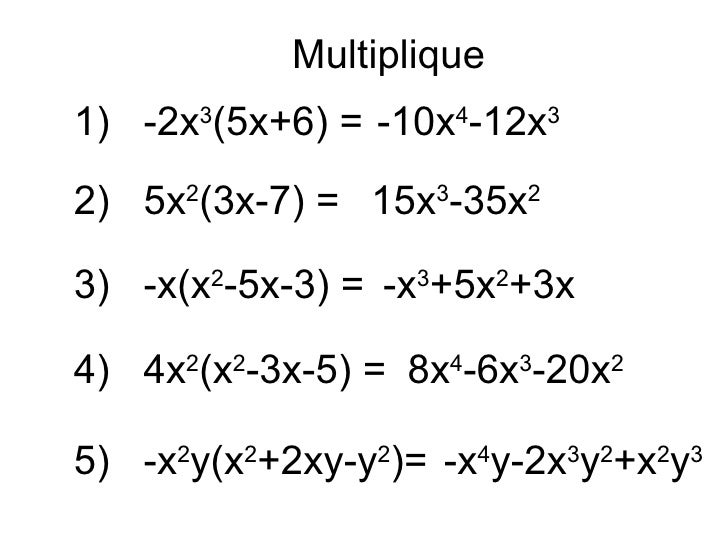
No hay comentarios.:
Publicar un comentario