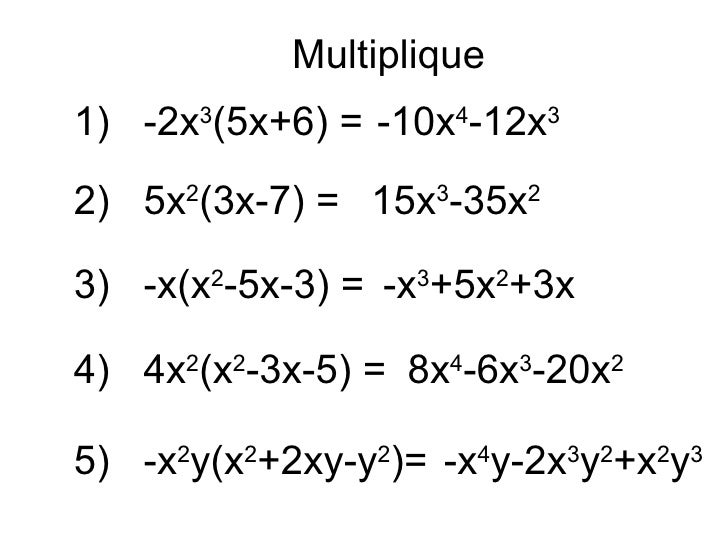LOS CONEJOS DE FIBONACCI
Se encontraba Alicia en el país de las maravillas junto con el Sr. Conejo y el matemago cuando de repente se encontró con un conejito.
_________________________________________________________________________________
-¡Un conejito!- dijo Alicia emocionada
-Una conejita- corrigió el matemago mientras ponía al conejito en el pasto - Dentro de un mes será adulta.
Cuando dijo esto, el matemago dio unas palmaditas a la conejita y esta aumento su tamaño
_________________________________________________________________________________
-¿A pasado un mes por arte de magia?- pregunto la niña asustada
-Para nosotros no, no te preocupes. Eh acelerado el tiempo vital de la coneja para no tener que esperar tanto. Para ella si que a pasado un mes: ahora es adulta y esta preñada, y dentro de otros meses tendrá una cría.
_________________________________________________________________________________
-¡Quiero verla!-dijo Alicia.
-De acuerdo.
El matemago dio otra palmada, y junto a la coneja apareció otra tan pequeña como la primera al salir del gorro.
-¿Dentro de otro mes será adulta y estará preñada?
-Si, y además su madre tendrá otra cría, pues desde que se hace adulta todas las conejas tienen una cría cada mes.

_________________________________________________________________________________
El matemago dio otra palmada. La cría creció junto a su madre y apareció otra conejita.
-No me digas, dentro de un mes la nueva conejita crecerá y las otras dos conejas tendrán una cría cada una- dijo Alicia
-Exacto- dijo el matemago. Dio otra palmada y sucedió lo que la niña habia previsto: por el suelo correteaban tres conejas adultas y dos crias. Otra palmada mas: cinco adultas y tres crias. Y otra: ocho adultas y cinco crias...
_________________________________________________________________________________
-¡Bravo!- aplaudio Alicia, pero paro- Menos mal que mis palmadas no hacen crecer y multiplicarse las conejitas, por que si no se habria llenado la habitacion.
-Pues si, la serie crece bastante rapido-
_________________________________________________________________________________
Vamos a verla: al principio: al principio habia solo un ejemplar, al cabo de un mes, seguia habiendo uno, al cabo de dos meses, ya eran dos, al cabo de tres meses, tres...
-Luego cinco- siguio Alicia-, luego ocho, y ahora ya son trece.
_________________________________________________________________________________
Cada vez que el matemago y Alicia nombraban los numeros, de sus bocas salia humo purpura que se convertia en numeros, quedando flotando en el aire ordenadamente.
_________________________________________________________________________________
-Como ves- dijo elmatemago- cada numero es la suma de los dos numeros anteriores: 2 = 1+1, 3 = 1+2, 5 = 2+3, 8 = 3+5, 13 = 5+8...
- Si das otra palmada, habra 21 conejitas, y luego 34 y luego 55...
_________________________________________________________________________________
- Exacto. Esta serie la descubrio Leonardo de Pisa, un gran matematico italiano del siglo XII, mas conocido como Fibonacci. Entre otras cosas, fue el quien impuso a Europa el sistema de numeracion arabe, que ya se conocia en España, y esta interesantisima serie se le ocurrio precisamente mientras pensaba enla reproduccion de los conejos.
______________________________________ñ___________________________________________
-¿Y para que sirve?
-Tiene importantes aplicaciones y aparece a menudo en la naturaleza. Por ejemplo, el crecimiento y la ramificacion de muchas plantas se produce de acuerdo con esta serie u otras similares, pues en realidad hay infinitas series de Fibonacci.
_________________________________________________________________________________
-¿Como son las otras?
-Si te fijas bien, la serie viene determinada por los dos primeros numeros, puesto que el tercero es la suma de ellos dos, el cuarto es el tercero mas el segundo, y asi sucesivamente. Si en vez de empezar con dos unos, partimos de otra pareja de numeros, obtenemos una serie distinta.
_________________________________________________________________________________
-Por ejemplo:
2, 2, 4, 6, 10, 16, 26, 42, 68, 110....
2, 1, 3, 4, 7, 11, 18, 29, 47, 76....
3, 2, 5, 7, 12, 19, 31, 50, 81, 131....
-¿Y el truco para sumar de prisa que me ibas a enseñar?
-Ahora mismo. Elige dos numeros de una cifra y escribelos uno encima del otro.
-El 4 y el 2- dijo Alicia, y las dos cifras quedaron flotando en el aire.
 4
4
2
_________________________________________________________________________________
- Ahora escribe debajo la suma de ambos
-El 6 dijo Alicia, y la cifra de humo ocupo su lugar correspondiente en la columna.
 4
4
2
6
_________________________________________________________________________________
-Ahora, debajo, la suma de 2 y 6.
-Es una serie de Fibonacci- dijo Alicia.
-Efectivamente. Te estoy haciendo el truco como si no conocieras esas series, pero puesto que ya las dominas, te dire simplemente que escribas , en columna, los diez primeros terminos de la serie de Fibonacci que empieza con los numeros 4 y 2.
-De acuerdo...
4 36
2 58
 6 94
6 94
8 152
14
22
__________________________________________________________________________
-Bien, pues la suma de esos diez numeros es 396- dijo el matemago en cuanto Alicia hubo terminado la lista.
-Has tenido tiempo de ir sumandolos mientras yo los escribia en el aire.
-Es cierto, pero no lo he hecho. He allado el resultado de forma instantanea, y tu tambien podras hacerlo en cuanto te explique el truco.
_________________________________________________________________________________
-¿Cual es?
-Es muy sencillo: si llamamos a y b a los dos primeros numeros, la serie sera esta- dijo el matemago, pasandolas paginas de su libro y mostrandole una columna de expresiones algebraicas.
a
b
a+b
a+2b
2a+3b
3a+5b
5a+8b
8a+13b
13a+21b
21a+34b
_________________________________________________________________________________
-No me gusta nada eso de mezclar letras con numeros- dijo Alicia-, pero esa lista esta bastante clara- admitio.
-Sumando todas las a y las b, veras que la suma de los diez terminos es 55a + 88b.
Pero fijate en el septimo termino de la serie: es 5a + 8b, luego la suma total es igual al septimo termino multiplicado por 11, puesto que 11 (5a + 8b) = 55a + 88b. Y multiplicar un numero de dos cifras por 11 es muy facil: sumas esas dos cifras y el resultado lo pones en medio, en este caso, 36 x 11 = 396, ya que 3 + 6 = 9.
-Ya veo- dijo Alicia- Para hallar la suma de cualquier lista de este tipo, no tengo mas que fijarme en el septimo numero, que es el cuarto empezando por abajo, y lo multiplico por 11.
_________________________________________________________________________________ -Muy bien. Y ahora, un espectacular truco de adivinacion matematica. Piensa un numero de tres cifras- dijo el matemago dandole la espalda
-Ya esta
-Dilo en voz muy baja para que yo no pueda escucharlo.
La niña susurro "236", y un hilillo de humo rojo salio de su boca y formo en el aire el numero con trazo muy delgado.
_________________________________________________________________________________
-¿Y ahora?
-Repite el mismo numero .
Alicia volvio a susurrar "236", y las tres cifras se juntaron a las anteriores para formar el numero 236,236.
-Ya esta
-Ahora divide por 7 ese numero de seis cifras. Hazlo en voz muy baja, para que yo no te oiga.
La niña musito para si la division, que fue realizandose en el aire a medida que iba nombrando los numeros y las operaciones. Al final obtubo 33,748 como cociente exacto.
_________________________________________________________________________________
-Ya he terminado. Menos mal que acabo de aprender la tabla del 7...
-Ahora divide el resultado por 11
Alicia dividio 33.748 por 11 y obtuvo 3.068.
-¡Vuelve a dar exacto!-dijo sorprendida.
-Y ahora divide el resultado por 13
-Es asombroso- dijo Alicia al terminar la division -da...
_________________________________________________________________________________
-El numero que habias pensado- concluyo el matemago volviendos. Y, efectivamente, en el aire flotaba un fino y luminoso 236.
-¿Como podias saberlo?
-Muy sencillo: escribir dos veces seguidas un numero de tres cifras equivale a multiplicarlo por 1.001. Y 7 x 11 x 13 =1.001. Si primero multiplicas un numero por 1.001 y luego lo divides por 1.001...
-Se queda igual- concluyo Alicia.
_________________________________________________________________________________
-Exacto. Un truco muy sencillo, pero de gran efecto. Te divertiras haciendoselo a tus amigos.
-Ya lo creo. Y los otros tambien me gustan. Seguro que mi profesor de matematicas no los conoce. Me vengare de el haciendoselos en clase.
-Ahora ya eres una pequeña matemaga - dijo el matemago, poniendole su sombrero en la cabeza-Sientate en el tronco.
Alicia se sento, y cuando el matemago le deposito el libro en el regazo reconocio su enigmatica sonrisa.
_________________________________________________________________________________
-¡Eres Charlie!- exclamo
La tunica y la barba blanca desaparecieron y ante ella aparecion Lewis Carrol con su melancolico y anticuado aspecto anterior.
-Si. La matemagia es una de mis mayores aficiones, y aveces me disfrazo para crear un poco de ambiente. Pero eres muy observadora y me has descubierto. Ya puedes despertar.
-¿Despertar?
-Si- dijo Charlie, mirandola con ternura y apoyandole una mano en el hombro- Despierta.
 En
éstos,
En
éstos, 













.jpg)